Preventing Sexual Harassment Through a Path Finding Algorithm Using Nearby Search
June 15, 2020

Path Finding Algorithm to Prevent Sexual Harassment Using Nearby Search
The results from this case study depend on previous work on heatmaps, which predict places at high risk of sexual harassment incidents. Below are simulations using Nearby Search and Directions API.
Again, this heatmap layer generated using gmaps Python package is completely simulated, but it does give insight into what potentially we could work with. Next, we need to find nearby ‘safespots’ and walking directions to those places using a pathfinding algorithm to prevent Sexual Harassment Cases. Thankfully, we can leverage Google’s Maps API for this — that is, the combination of both Nearby Search and Directions API:

Figure 2: Hospitals found within 800m walking distance using Nearby Search (Point A is the origin, Point Bs are destinations)
To quickly detail what was done here:
- Used Nearby Search API to find the nearest hospitals within 800 meters
- Nearby Search to create a list of coordinates for these locations
- Directions API to find walking directions to these places
If you do want to take a look and try it out on your own, check out here for the Nearby Search API and here for the Directions API .
At this time, my fellow team members informed me they have pushed a working version of the heatmaps model to prevent sexual harassment cases and that we were able to incorporate the first version of the heatmap; so away with the simulated heatmap, and here is what it actually looks!

Figure 3: Heatmaps of predicting sexual harassment incidents in Mumbai
A few quick points about this figure:
- Given latitude, longitude boundaries and a 28 by 28 array of risk scores, we interpolate the specific coordinates of each spot or ‘grid point’ to create this lattice-looking overlay (coordinate calculations were done using haversine)
- Risk scores are discrete, ranging from 0 to 4, with 0 being the safest of spots and 4 being the most dangerous
- Area of each ‘grid point’ works out to be ~1.74 km² (which is fairly large, meaning the resolution isn’t the finest)
Let’s now superimpose the directions layer on top of this and see what we’re working with:

Figure 4: Nearby hospitals within 800 meters walking distance of Point A
As you can see, various hospital locations are located within 800 meters; however, it is quite intuitive to any user looking at this to avoid the top-side locations, since the risk scores are higher (illustrated by warmer colors). Looking at this, one can simply make a decision on where to go by:
- Prioritizing the overall route safety-ness
- Choosing the closer location
Computing the risk associated with taking each route and finding the safest using heatmap analysis to prevent sexual harassment cases
However, in times of where the user is in stress and needs to make a decision immediately, such cognitive abilities come as a luxury (this is akin to determining which route to take with only traffic data provided). The application should complete these tasks for the user, and thus we’ve come to the crux of the problem:
How can we determine the safety-ness of routes?
Again, working our way from simple to more complex solutions, we can:
- Determine overall route safety-ness solely by the risk score associated with the destination
- Calculate the average of risk scores based upon grid coverage of the straight-line path from origin to destination
- Calculate the average of risk scores based upon grid coverage of each step of the route to get to the destination
Completing the first solution isn’t too complicated — in short, you have coordinates for each grid point and finding the grid point that is closest your destination to obtain its risk score involves finding the one with shortest Euclidean distance (here we use a linearized method and assume there’s no curvature between points for simplicity).

Figure 5: Euclidean distance between points a and b
Taking on the second and third solutions requires leveraging external resources — we can reframe this problem as one that involves determining the line-of-sight. For example, how can a one determines if their vision is blocked by obstacles; in this context of finding the best route, how do we know if a route touches a grid point? Equipped with the knowledge that there’s pretty much an algorithm for everything, we turn to Bresenham’s line drawing method.
Bresenham’s line algorithm is a line drawing algorithm that determines the points of an n-dimensional raster that should be selected in order to form a close approximation to a straight line between two points.
Computer graphics work in units of pixels, so we can see how this path finding algorithm originated from the need to shade in pixels graphical operations.
The general idea behind this algorithm is: given a starting endpoint of a line segment, the next grid point it traverses to get to the other endpoint is determined by evaluating where the line segment crosses relative to the midpoint (above or below) of the two possible grid points choices
As an attempt to walk through this method, we’ll study the following diagram:

Figure 6: Demonstration of Bresenham line drawing algorithm (courtesy of Rochester Institute of Technology)
- Here, we assume the points refer to each grid point (which are the center point for each grid box)
- Assume we have a line segment spanning from left to right in upward slope fashion (smaller (x, y) to larger (x, y) coordinates). Let us also say that the initial grid point P is shaded and has already been determined to be traversed through
- Consider point P as the previous grid point, we then need to determine the current grid point to be shaded. To do so, we also consider the grid points E and NE (for east and northeast of the current grid point, respectively)
- M is the midpoint between E and NE
- Based on where the line segment intersects between the line between E and NE and the point of intersection relative M (above or below M ), we can make a decision on the current grid point that the line traverses through, which is NE in this case, as the line intersects above M
- The grid points E and NE (and consequently, M) are then updated in reference to the current grid point and the same methods above are applied again and again until we reach the opposing endpoint of the line segment
When we complete the process of the pathfinding algorithm, we arrive at something like this:
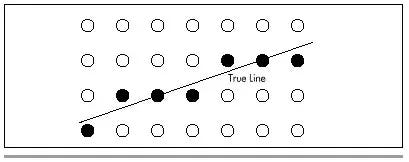
Figure 7: Shaded-in grid points using Bresenham’s algorithm
Fortunately, we need not code this out from scratch as skimage already has an implementation of this — here’s a small snippet of what the code looks like:
from skimage.draw import line import matplotlib.pyplot as plt # create array of zeros example_arr = np.zeros((10, 10)) # set endpoints for line segment x0, y0 = 1, 1 x1, y1 = 7, 9 # draw the line rr, cc = line(y0, x0, y1, x1) example_arr[rr, cc] = 1 # plot it out plt.figure(figsize=(8, 8)) plt.imshow(example_arr, interpolation='nearest', cmap='viridis') plt.plot([x0, x1], [y0, y1], linewidth=2, color='r')

Figure 8: Illustration of Bresenham’s line drawing method using skimage and matplotlib
As you can see, the approximations of the grid point shading are imperfect, as there are definitely grid points that the line has crossed that are not shaded in.
Of course, there’s another pathfinding algorithm to improve on this where all of the points that are crossed are shaded in; I won’t go in detail here but the term used is to find the supercover of the line segment:

Figure 9: Method for finding the ‘supercover’ of a line segment
Zooming back out to our problem at hand here, we apply these grid coverage methods to compute the average of risk scores of steps for each route to determine the best. We prioritize the safety of the route first, before accounting for the distance (i.e. the safest route is suggested first if two routes are tied in safety-ness, we then suggest the closer destination), using heatmaps analysis to prevent sexual harassment cases.
To top it off, we apply this method to our heatmap to illustrate how one route could look like:

Figure 10: Route determined using line drawing methods between two points
This article is written by Daniel Ma.
You might also like





